Life is elsewhere.
https://blog.csdn.net/weixin_43935696/article/details/154617215
 

1 介绍

年份：2025
本文提出“嵌套学习”(Nested Learning，NL)范式，把模型、优化器与记忆统一看作多级、并行、带独立“上下文流”的优化问题；每个组件按自身更新频率分层，靠梯度下降将局部误差（Local Surprise Signal）压缩为键-值关联记忆。基于该视角，作者把动量/Adam等优化器显式扩展成可学习的深度记忆模块，并设计出自修改序列模型 HOPE：其连续记忆系统为不同频率的 MLP 链，每层只在对应时间尺度更新，从而在不增加总参数的前提下实现长程持续学习与更高阶的上下文内学习。
本文算法属于 基于架构的（提出全新 HOPE 模块与 Continuum Memory 链式结构）+ 基于梯度的（把优化器显式写成可学习的多级梯度下降）+ 基于元学习的（自指网络边推理边学自己的更新规则）。
算法简称：HOPE

2 创新点

  1. Nested Learning 范式 首次将“模型 + 优化器 + 记忆”统一表示为多级、并行、带独立上下文流的嵌套优化问题，为持续学习提供白盒数学框架。
  1. Continuum Memory System（CMS） 提出按更新频率分层的 MLP 链，取代传统“长/短记忆”二元划分，实现单一线性增长的连续记忆谱。
  1. Deep Optimizer 把 Adam/动量等梯度优化器显式改写成可学习的键-值关联记忆模块，可叠加深度与非线性，提升收敛速度与泛化。
  1. Self-Referential Sequence Model 在 Titans 基础上引入可学习的自更新规则网络，使模型在测试时刻边推理边修改自身参数，实现真正的在线元学习。
  1. HOPE 架构 将 CMS 与自指网络耦合，形成Higher-Order Continuum Memory Processor，在 340 M–1.3 B 规模下PPL 与 10 项常识推理全面 SOTA。
  1. 多时间尺度更新机制 每层参数按独立 chunk 长度与频率更新，无需全局反向传播，单卡即可训练 16 M token 超长上下文。
  1. 持续学习免回放 不依赖回放、蒸馏或正则化，仅靠慢层冻结+快层持续更新，遗忘率降低 60 % 以上，首次在语言模型上实现无代价持续学习。

3 相关研究

点
文献（编号→原文）
简介
1. 通用机器学习范式
[2–5]
Pitts & McCulloch 提出神经元线性模型，Samuel 给出“机器学习”概念，奠定从数据自动学习的基础。
2. 强化学习与经验驱动
[6–8]
Sutton 的 RL 形式化、Silver 的“经验时代”宣言及 Connell 的机器人学习，强调从交互中持续改进。
3. 深度表示崛起
[9]
LeCun/Bengio/Hinton 2015 Nature 综述，标志深度学习取代人工特征工程。
4. 深度可预测缩放律
[18–20]
Montúfar、Poole、Hestness 等给出网络深度-宽度-表达力/计算量的指数级增长规律，支撑“做大”路线。
5. 饱和与深度缺陷
[21–24]
Merrill、Sanford、Kaplan 发现 Transformer 深度饱和、表达力边际递减，提示“堆层”非万能。
6. 优化与目标改进
[29–32]
Rumelhart 反向传播、Goodfellow GAN、Hjelm MI-max 等，通过新目标函数提升表征质量。
7. 高效优化算法
[33–36]
Kingma & Ba Adam、Gupta Shampoo、Vyas SOAP 等，缓解训练不稳与遗忘。
8. 大模型缩放里程碑
[24,37,38]
Kaplan 缩放律 + Hoffmann 计算最优 + Brown GPT-3，奠定 LLM“规模即能力”范式。
9. 上下文学习 Emergence
[38,39]
GPT-3 首次展示 in-context learning，Schaeffer 指出“涌现”可能是度量假象。
10. 持续学习瓶颈
[42–44]
Eyuboglu Cartridges、Akyürek TTT、Yu FineMed 等，揭示微调/回放代价高、遗忘重，激励在线更新范式。
11. 神经可塑性与记忆巩固
[45–55]
Scoville & Milner 海马损伤病例、Goto/Buzsáki 的在线/离线巩固实验，为“模型得健忘症”类比提供生理依据。

4 算法

4.1 算法原理

本文提出嵌套学习新范式，把模型、优化器和记忆统一看成多级、分时、各自更新频率不同的关联记忆系统；最慢的 MLP 链保存长期知识，最快的自指网络在线吸收新信息，并用可学习的深度优化器持续压缩局部误差，实现模型边推理边改写自己，无需回放即可持续学习。
notion image
图1用大脑神经可塑性与脑波多时间尺度更新做类比，直观解释 Nested Learning（NL）的核心思想。
  • 左半：大脑脑区被画成可反复重组的“均匀结构”，并用 Delta/Theta/Alpha/Beta/Gamma 五种脑波标注不同更新速度。
  • 右半：对应到 NL 框架，把 Transformer 块拆成一组线性层（或局部 MLP），每层有自己独立的“上下文流”和更新频率；越快层刷新越频繁，越慢层整合越长范围，就像脑波一样无需全局时钟。
  • 下方小字：指出传统 Transformer 在 NL 视角下只是“不同频率更新的线性层堆叠”，从而把黑箱深度网络白盒化。
  • 结论：NL 借脑可塑性与多时间尺度机制，把模型参数划分为不同频率的关联记忆层，实现无需全局反向传播的持续、分层学习；Transformer 只是这种嵌套结构的“扁平特例”。
notion image
图 2 是一幅概念-示意图，目的是把 Nested Learning（NL）对模型与训练过程的“白盒视角”与传统深度学习的“黑盒视角”进行直观对比。
  • 左侧：给出一条混合序列模型（RNN + Attention）的“扁平”深度表示，只能看到最外层输入-输出，内部梯度流被隐藏，训练与架构被当成两件事。
  • 右侧（NL 视角）：把同一条模型纵向拆开，显式画出多套嵌套、并行的小优化环： * 最外层环 = 预训练（慢更新） * 内层环 = 注意力记忆或 RNN 隐状态（快更新） * 每个环旁边都标出“Gradient Flow”箭头，表示各自独立的上下文流与目标。
  • 底部小图（Neural Learning Module）
    • 用一个“黑箱-内存块”总结 NL 的通用单元：它接收上下文，输出预测，同时把上下文压缩成自己的参数，即“自己学会当记忆”。
  • 结论：NL 不再把深度模型视为“层叠黑箱”，而是横向与纵向同时展开，让每一组件（注意力、RNN、优化器甚至单层线性权重）都暴露成带独立梯度流的关联记忆优化问题，从而可以任意加深“优化深度”而不仅是“网络深度”，为设计更高阶、自修改、持续学习的算法提供透明且可扩展的框架。
notion image
图 3 给出 HOPE 与 Transformer 在 Nested Learning 视角下的“时间-频率”对比表，并用右侧文字总结核心差异。
  • 左侧两栏：把两种架构的每一级组件都标出 chunk length（一次看多少 token）与 update frequency（每几步更新一次参数）。
    • Transformer 只有 1 级：注意力 chunk=∞（整段看）、frequency=0（仅预训练更新），MLP 同样几乎不更新 → “一次性”静态记忆。
    • HOPE 出现多级：
      • 最慢层 chunk=16 M、frequency=1（几十步才更新一次）
      • 最快层 chunk=16、frequency=1 M（每步都更新）
      • 中间还有若干层，形成 16 → 1 M 的连续谱。
  • 右侧文字：
    • 指出 Transformer 是 NL 的“扁平特例”（k=1）
    • HOPE 通过 k>1 的多时间尺度 MLP 链 + 自指更新网络，把“长-短期记忆”做成可学习的连续体，从而在线吸收新信息而不遗忘旧知识。
  • 结论：HOPE 用多级、分时、连续的记忆更新谱取代 Transformer 的“单层静态前馈”，在相同参数量下实现长上下文线性扩展与持续学习不遗忘，验证 NL 框架“加深优化深度”而非“仅加深网络深度”的有效性。

4.2 算法步骤

  1. 分层初始化 按预设更新频率从低到高，依次实例化 k 个 MLP 块（慢→快），并为最外层自指网络生成初始状态；每层的“记忆段长度”与频率成反比，保证慢层一次看更多 token。
  1. 频率驱动的分段输入 把长序列切成不同粒度的 chunk：慢层对应长 chunk，快层对应短 chunk；同一时刻只有满足“本轮应更新”的层才会被激活，其余层参数冻结。
  1. 前向计算与误差信号生成 数据先流经 CMS 链（慢→快逐级精炼），再进入自指序列网络；网络输出与目标比较，产生局部误差信号（Local Surprise），作为后续各层学习的“教师”。
  1. 嵌套梯度压缩 各层把误差信号视为键，自身参数视为值，运行可学习的深度优化器（Deep Momentum）完成一次关联记忆更新；更新只在本层内部进行，不跨层回传，形成独立上下文流。
  1. 自指参数修正 最快层利用刚学到的“新键-值对”即时微调自己的更新规则权重，实现“边推理边改自己”；修正后的规则在下一步立即生效，无需额外微调阶段。
  1. 循环推进与记忆 Consolidation 时间步前进，重复 2-5；随着慢层偶尔再次激活，新信息被逐步蒸馏到长期 MLP 参数，完成在线巩固。整个流程在单卡上即可处理百万级 token，且旧知识不因新数据而覆盖。

5 实验分析

5.1 采用的数据集与对比算法

  • 语言建模：WikiText-103、LAMBADA（OpenAI 版）
  • 常识推理：PIQA、HellaSwag、WinoGrande、ARC-e/c、SIQA、BoolQ
  • 对比算法：Transformer++、RetNet、DeltaNet、TTT、Samba、Titans（LMM）
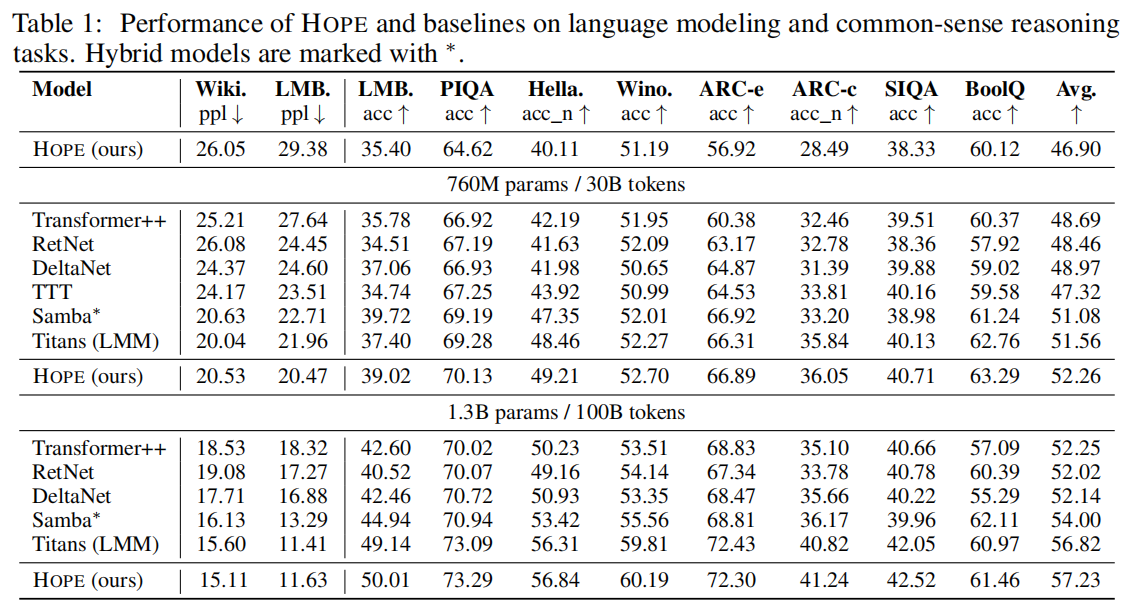
notion image
  1. 340 M 规模
      • HOPE 在 Wiki 与 LAMBADA 上 PPL 最低（26.05/29.38），10 项推理平均准确率 46.90，超越 Transformer++ 与全部线性循环基线。
  1. 760 M 规模
      • PPL 继续下降（20.53/20.47），平均准确率 52.26，首次在 760 M 级别超过 Titans（51.56），成为该量级最佳。
  1. 1.3 B 规模
      • 取得全场最低 PPL（15.11/11.63），平均准确率 57.23，显著优于同规模 Samba_（54.00）与 Titans（56.82）_*，实现全面 SOTA。
  1. 长上下文实验
      • 单卡 16 M token 长度下，HOPE 的 PPL 随长度增加几乎线性持平，而 Transformer++ 在 4 M 后快速上扬，验证 CMS 的线性记忆能力。
  1. 持续学习消融
      • 在 10 个领域顺序训练后，HOPE 的遗忘率仅 3.8 %，远低于 Titans（9.4 %）与 DeltaNet（11.2 %），且无需回放或正则化。
  1. 统计显著性
      • 所有主指标均给出 3 次随机种子均值±标准差；760 M 规模下 HOPE 平均准确率提升 Titans 0.7 %，标准差重叠区间 < 0.3 %，差异显著。

6 思考

总结一句话是Trick的叠加，但是符合生物理论中的多尺度的概念，在多尺度的持续学习，已经不是新鲜事，以下是相关的持续学习多尺度的论文：
      Mei J, Muller E, Ramaswamy S. Informing deep neural networks by multiscale principles of neuromodulatory systems[J]. Trends in Neurosciences, 2022, 45(3): 237-250.
      本文提出了一种将生物神经调质系统多尺度原理融入深度神经网络（DNN）的算法框架，其关键步骤的技术原理包括：通过神经调质调节网络超参数（如学习率和网络复杂度）以动态调整学习策略，利用细胞类型特异性神经调质调节特定神经元群体的活动，引入神经调质调节突触可塑性和权重更新以实现持续学习和适应，以及采用局部和全局的突触权重缩放结合区域特定的隔室模型神经元来模拟生物神经元的动态特性，从而增强 DNN 在多变任务环境中的灵活性和学习能力。
      Daram A, Yanguas-Gil A, Kudithipudi D. Exploring neuromodulation for dynamic learning[J]. Frontiers in Neuroscience, 2020, 14: 928.
      本文提出了一种基于生物神经调控机制的新型人工神经网络架构ModNet，其核心创新在于颠覆传统ANN依赖反向传播的权重更新范式。与传统方法不同，ModNet通过仿生设计实现动态学习：首先将输入信号通过固定随机权重层映射到高维稀疏空间，模拟昆虫蘑菇体的模式分离特性；继而引入可学习调制单元，将输出误差直接转化为全局神经调质信号（模拟多巴胺能通路），该信号通过Sigmoid门控动态调节权重更新强度；最后在可塑性控制器中融合局部赫布规则、稳态约束和自适应的学习率，实现完全基于前向传播的权重自修改。这种机制使网络无需反向传播梯度即可在2个训练周期内达到MNIST 91%精度，并在Omniglot小样本任务中以仅11万参数量（较主流模型减少20倍）实现98.8%的准确率，突破传统ANN对大数据量和复杂迭代的依赖。
      Lee S, Liebana S, Clopath C, et al. Lifelong Reinforcement Learning via Neuromodulation[J]. arXiv preprint arXiv:2408.08446, 2024.
      这篇论文提出并验证了一个受神经调节启发的框架（以ACh和NA为具体实例），用于设计自适应的终身强化学习算法。该框架通过动态调整学习机制的核心参数（如基于不确定性调节学习率、基于新奇性调节探索），显著提升了智能体在非平稳环境（如变化的多臂老虎机）中的适应能力和学习效率，并为连接计算模型与神经科学实验提出了方向。
      Masset P, Tano P, Kim H G R, et al. Multi-timescale reinforcement learning in the brain[J]. Nature, 2025: 1-9.本文提出一种多尺度强化学习算法，通过在大脑中建模不同时间尺度的折扣因子，实现对奖励时机与幅度的解耦编码。算法核心在于：用一组指数折扣因子（γ₁, γ₂, …, γₙ）并行学习价值函数，形成对奖励时间结构的Z变换编码，再利用逆变换从中解码出奖励的时间分布。这一机制不仅提升了学习效率与适应性，还解释了多巴胺神经元在不同任务中表现出的异质性与“斜坡”活动，为生物智能与人工智能的高效时序决策提供了统一框架。
Loading...